My Projects

Here are some theoretical projects that I’ve worked on. Currently the list is a bit old, but expect more projects to be here soon.

Math

The Galois Correspondence in Algebraic Topology

[Twoples, Fall 2020] One of the central objects that connects algebra with topology is the fundamental group. Infact, there is a very surprising relationship between the lattice of covering spaces of a topological space and the lattice of subgroups of its fundamental group, given that the space in question is sufficiently nice. In this reading project, I studied this relationship briefly. A poster was made for the same.

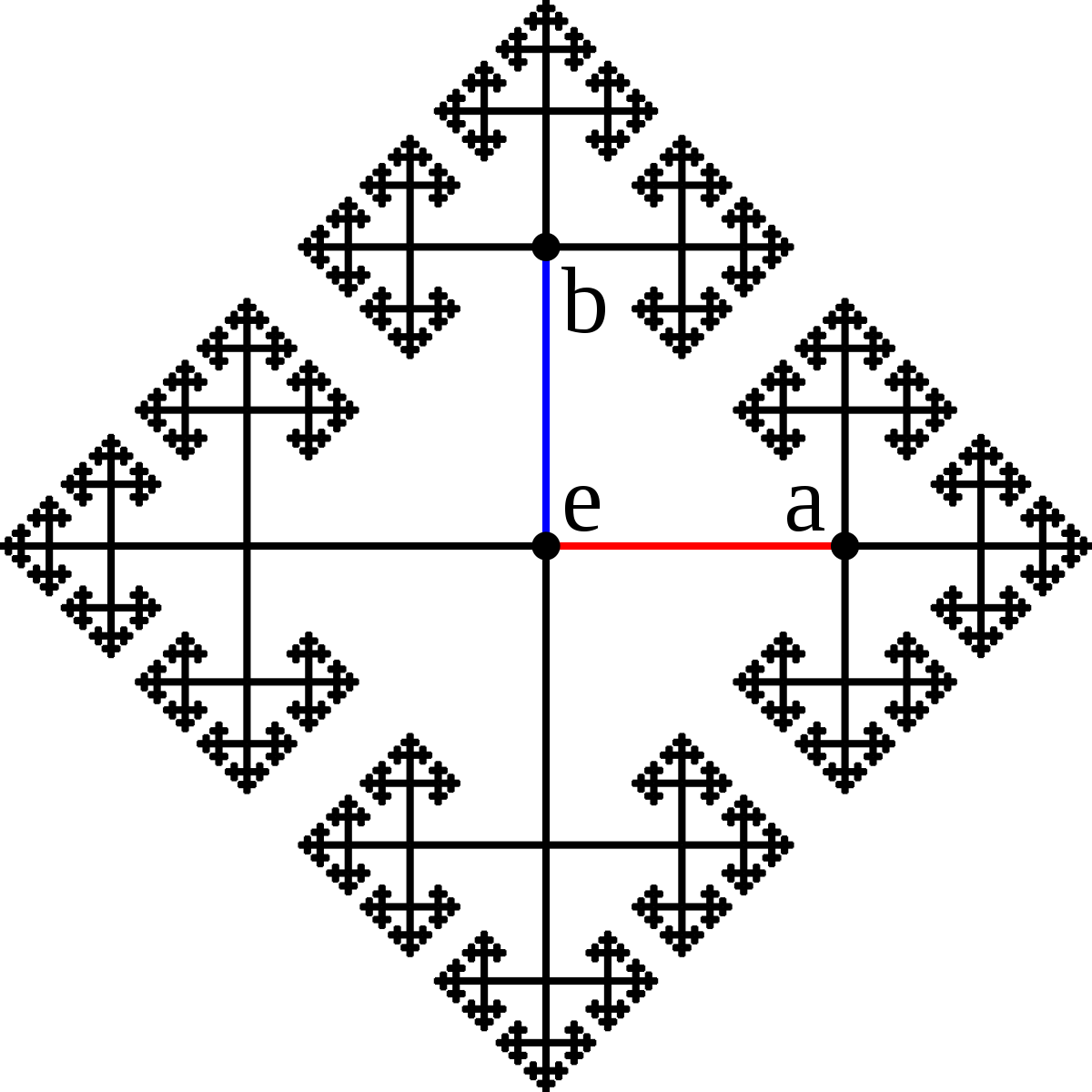
The picture above represents the Cayley graph of the free group $\langle a,b\rangle$ on two generators, which is a standard picture in algebraic topology.

The Bernoulli Sandpile on the Infinite Ladder.

[PROMYS, July-August 2019] A sandpile is a graph in which each vertex contains grains of send and is allowed to topple, i.e send one grain of sand to each of its neighbors. We studied the toppling behavior of random sandpiles on the ladder graph $\mathbb{Z}\times\mathbb{Z}_2$, with a bernoulli distribution on the number of grains of sand on each vertex. A poster was made by my partner, and we also made a presentation for exhibiting our work.

This represents a mod-1 harmonic function on the ladder, where $\alpha$ is a carefully calculated number.